재귀관계
재귀 = 원래의 자리로 되돌아가거나 되돌아옴.
재귀 호출 = 자기자신을 호출
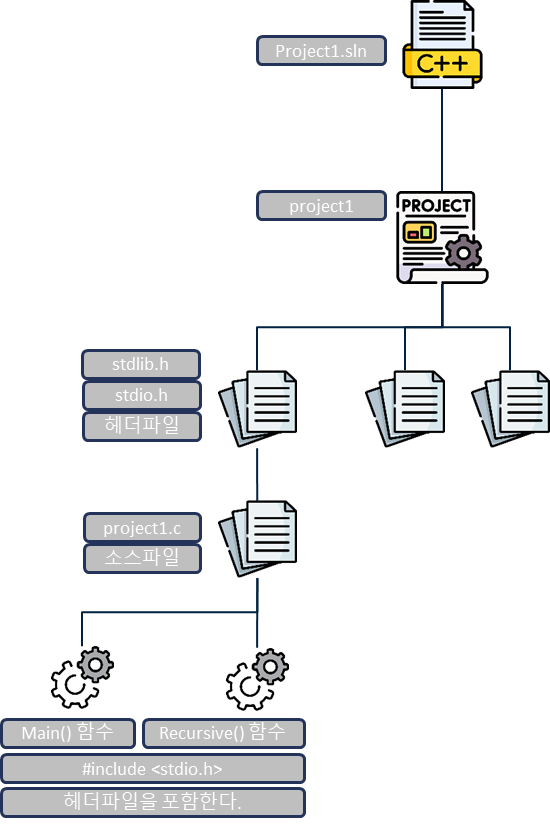
함수의 재귀적 호출의 이해
함수
스파게티 먹고 싶다()
{
면삶기();
면투척();
...();
}
면삶기(), 면투척(), ...이걸 한줄로 설정하고 싶을 때 함수를 사용
매크로
단축된 단어로 긴 함수를 불러오는 것
매크로 함수를 이용해 main()함수의 코드를 줄 일수 있다.
재귀함수
그럼, 함수가 함수 자신을 불러오는 것이 재귀함수라는 것을 이해할 수 있을 것이다.
but, 재귀함수의 문제점부터 알아보자
우선 구조를 이해해야 한다.



재귀를 사용할 때 탈출조건을 만들어줘야 한다.
재귀함수(탈출 조건 O)



if(num<=0) //재귀의 탈출 조건
return; //재귀의 탈출!
함수가 종료되면 그 함수는 호출된 지역으로 다시 돌아간다.

factorial 함수
return함수를 주의해서 보자



피보나치 수열을 통한 재귀함수


앞에 두 항을 더하면 다음 항이 결정된다.

0 1 1 2 3 5 8...순으로 진행되므로 5번째 항의 결과값은 3이 된다.


피보나치 함수는 이러한 과정으로 진행이 된다.
f(5)를 호출할 때마다 많은 처리를 해야 되서 비효율적이다.
그러면 좀 더 효율적으로 하려면 어떻게 해야 할까?
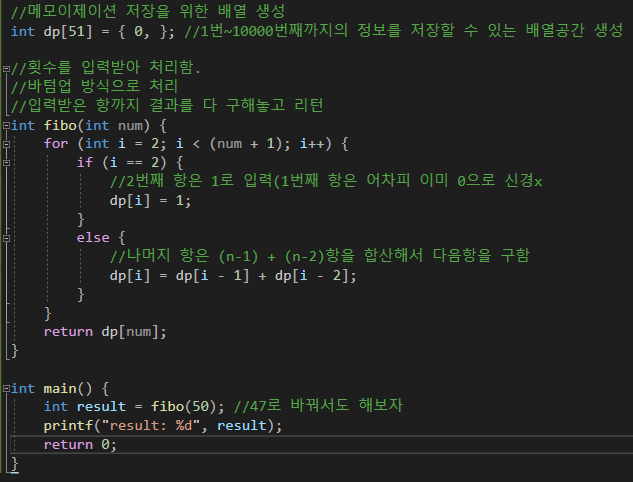
재귀호출없이 메모이제이션을 활용하면 된다.(=바텀 업)
메모이제이션
장점은 저장한 설 불러와서 계산해 호출 메모리 낭비가 줄어든다.
단점은 저장공간을 희생한다. (저장공간이 추가로 필요하다.)
하지만 과거에는 저장공간이 귀했지만 요즘은 메모리가 안귀한 시절이 왔기 때문에 시대적으로 봤을 때 더 효율적이다.

피보타치 재귀호출은 비효율적이라고 볼 수 있다. 이를 해결하기 위해서 동적계획법(=바텀 업)을 활용한다.
HanoiTowerMove(3, 'A', 'B', 'C');
3개도 해봐라


메모리에 저장해서 불러와 호출하는 방식 = 메모이제이션
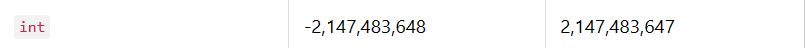

int로 최대로 표현할 수 있는 걸 넘어서서-(마이너스)가 출력된다.

동적계획법들을 주로 쓰지만 재귀호출로만 풀 수 있는 문제들이 있기 때문에 재귀함수를 쓰지 않는 것은 아니다.
그것이 하노이의 탑이 대표적이다.
하노이의 탑

쌓아 놓은 원반을 최소의 횟수로 옮기기 위한 알고리즘
모든 원반을 세 번째 기둥으로 최소의 횟수로 옮긴다.
원반은 1개씩만 옮길 수 있으며, 큰 원반을 작은 원반 위에 쌓을 수 없다.
<'시작 기둥', '중간 기둥', '목표 기둥'>

가장 큰 원반을 목표 기동으로 옮기려면 나머지를 중간 기동으로 옮겨야 한다.
1. 가장 큰 바닥 원반을 제외한 나머지를 시작 기동에서 중간 기둥으로 옮긴다. (재귀호출)
2. 바닥 원반을 시작 기중에서 목표 기둥으로 옮겼음을 출력한다.
3. 바닥 원반을 제외한 나머지를 중간 기동에서 목표 기동으로 옮긴다. (재귀 호출)
'자료구조' 카테고리의 다른 글
| 자료구조 <추상화와 구조체> (0) | 2023.08.22 |
|---|---|
| 자료구조 <메모리 영역> (0) | 2023.08.22 |
| 자료구조 <변수> (0) | 2023.08.22 |
| 자료구조 <이진탐색> 알고리즘 이해 (0) | 2023.08.16 |
| 자료구조 <선형탐색> 알고리즘 이해 (0) | 2023.08.16 |